import numpy as np
import pandas as pd 
import seaborn as sns
%autosave 20

Autosaving every 20 seconds

통계량의 분포

모집단과 표본

자료분석의 목적은 모집단에 대한 특성 파악을 위한 것임.
관심있는 모집단의 크기가 너무 커서 자료를 조사할 수 없음.
따라서 모집단의 일부분인 표본을 추출하고 추출된 표본에서 얻은 정보, 즉 표본 통계량을 이용하여 모집단의 특성을 추론

예시 - 선거 여론조사

목적
- 모든 선거구 주민(\(P\),population)의 후보 A에 대한 모집단의 지지율 파악
모집단의 특성 (관심있음)
- 후보 A에 대한 지지율

\[\text{모집단의 지지율} = \frac{\text{모집단에서 후보 A를 지지하는 사람의 수}}{모집단에 속한 사람의 수}\]

근데 이걸 조사할 수 있음? NONO, 너무 커서 절대 불가능 함
따라서 표본을 추출하고 표본 지지율로 모집단의 지지율에 대한 정보를 얻음.

\[\text{표본 지지율} = \frac{표본에서 후보 A를 지지하는 사람의 수}{표본에 속한 사람의 수}\]

용어정리

용어	기호	정의	예
모집단(population)	P	관심이 있는 전체집단	모든 선거구 주민
모집단의 수	N	전체집단에 속한 개체 수	모든 선거구 주민의 수
모수(parameter)	\(\theta\)	모집단의 특성값	모집단의 지지율
표본(sample)	S	모집단의 부분 집합	표본으로 추출된 주민
표본의 수	n	표본에 속한 개체의 수	표본으로 추출된 선거구 주민의 수
표본 통계량(sample statistics)	\(\hat{\theta}\)	표본의 특성값	표본 지지율

모수(parameter)는 모집단의 특성을 나타내는 값으로 분석의 목적에 따라 다양하다.
- e.g.
  - 전북대학교 남학생의 키를 분석하는 것이 목적 \(\to\) 모수는 평균
  - A후보의 지지율을 분석하는 것이 목적 \(\to\) 모수는 비율
표본 통계량(sample statistics)은 표본의 특성을 나타내는 값이다.
- 추정량(estimator) 또는 검정 통계량이라고 부르기도 한다.

모집단?표본?

모집단

모집단이 아래와 같다고 하자.

\[P = \text{{철수,영이,둘리,흥민,연경}},N=5\]

관심있는 모수 \(\theta\) : 후보 A에 대한 지지율

\[\theta = \frac{\text{모집단에서 후보 A를 지지하는 사람의 수}}{\text{모집단에 속한 사람의 수}}\]

모집단에 속한 5명이 선거 후보 A에 대한 지지 여부…
- 철수 = 지지 = (\(x=1\))
- 영이 = 지지 = (\(x=1\))
- 둘리 = 지지 = (\(x=0\))
- 흥민 = 지지 = (\(x=0\))
- 철수 = 지지 = (\(x=1\))
이와 같은 경우 모집단 지지율 \(\theta\)는 다음과 같다.

\[\theta = \frac{3}{5} = 0.6\]

표본

5명의 모집단에서 단순임의추출로 3명의 표본을 비복원추출하는 경우를 생각해 보자.
지지하면 \(x_i = 1\) 지지하지 않으면 \(x_i = 0\)이라고 하자.
표본지지율은?

\[\hat\theta = \frac{표본에서 후보 A를 지지하는 사람의 수}{표본에 속한 사람의 수} = \frac{\sum_{i=1}^{3}x_i}{n} = \bar x\]

크기가 5인 모집단에서 크기가 3인 표본을 추출 할 때, 모든 가능한 표본은 몇 개일까? \(\to\) 조합으로 계산

\[{{N}\choose{n}} ={{5}\choose{3}} = \frac{(5)(4)(3)}{(3)(2)(1)} = 10\]

5명의 사람들로 구성된 모집단에서 나타날 수 있는 모든 경우의 표본을 계산해보자.

from itertools import combinations

P = ['철수', '영이', '둘리', '흥민', '연경'] 

N = len(P)
n = 3

all_possible_samples = []
all_possible_samples_text = []

for sample in combinations(P, n):
  all_possible_samples.append(sample)
  txt = ""
  for i,name in enumerate(sample):
    if i == len(sample) -1:
      txt += name
    else:
      txt+= name + ","
  all_possible_samples_text.append(txt)
all_possible_samples_text

['철수,영이,둘리',
 '철수,영이,흥민',
 '철수,영이,연경',
 '철수,둘리,흥민',
 '철수,둘리,연경',
 '철수,흥민,연경',
 '영이,둘리,흥민',
 '영이,둘리,연경',
 '영이,흥민,연경',
 '둘리,흥민,연경']

all_possible_num = len(all_possible_samples)
all_possible_num

통계량의 정확한 분포

우리가 궁극적으로 알고자 하는 것은 모집단의 특성값인 모수이다.
통계학에서는 표본으로부터 계산하는 표본통계량으로 부터 모수를 추정한다.
- 그러므로 표본통계량 자체의 성질,특징에 대해 이해하는 것 자체가 중요하다.
  - 좀 더 상세히 하자면 표본통계량은 표본이 임의적(random)으로 추출되기에 임의성(randomness)를 가지는 확률변수이므로
  - 표본통계량(확률변수)의 확률분포를 파악하여 확률적 성질,특징을 파악하는 것이 중요하다.
- 뿐만아니라 추후에 나올 방법들은 확률적 성질,특징을 통해 모수를 추정한 방법이 얼마나 합리적인지 판단에 도움을 준다.
그렇기에 우리는 표본통계량의 분포를 알아야 한다.
목적 : 표본통계량은 모수를 적절히 추정하는데 핵심이다. 이것이 갖는 성질,특징을 잘 파악하여 합리적인 추정을 하기위해 표본통계량의 분포를 구해보자.
따라서 표본으로부터 계산한 표본통계량도 random하며 확률변수이다.
그렇다면 표본 통계량의 분포는 어떻게 되는가?
1. 가능한 모든 표본통계량의 값과
2. 각각의 값에 대응하는 확률을 알아야 한다.

(가능한 모든 표본 통계량의 값 구하기)

from fractions import Fraction

support = {'철수':1, '영이':1, '둘리':0, '흥민':0, '연경':1}
sample_rate = []
for i,sample in enumerate(all_possible_samples):
  total = 0
  for obj in sample:
    total += support[obj]
  sample_rate.append(Fraction(total,3))

sample_rate

[Fraction(2, 3),
 Fraction(2, 3),
 Fraction(1, 1),
 Fraction(1, 3),
 Fraction(2, 3),
 Fraction(2, 3),
 Fraction(1, 3),
 Fraction(2, 3),
 Fraction(2, 3),
 Fraction(1, 3)]

from itertools import combinations
P = ['철수', '영이', '둘리', '흥민', '연경'] 

N = len(P)
n = 3

all_possible_samples = []

for sample in combinations(P, n):
    all_possible_samples.append(sample)

all_possible_samples
P = np.array([1,1,0,0,1]) 
n=3

all_possible_samples = []
for sample in combinations(P, n):
    all_possible_samples.append(sample)

all_possible_samples

sample_rate = []

for sample in all_possible_samples:
  sample_rate.append(Fraction(int(sum(sample)),n))

sample_rate

sample_rate_dist = pd.DataFrame({'sample_rate':sample_rate, 'probability': np.repeat(1/all_possible_num, all_possible_num)})
sample_rate_dist

sample_rate_dist.groupby(by=sample_rate).sum().reset_index().rename(columns = {'index':'sample_rate'})

	sample_rate	probability
0	1/3	0.3
1	2/3	0.6
2	1	0.1

(각각의 표본통계량에 대응하는 확률 구하기) - 아래의 데이터 프레임은 가능한 모든 표본으로부터 계산한 통계량과 각각의 표본이 뽑힐 수 있는 확률을 나타낸다.

sample_rate_dist = pd.DataFrame({"sample(outcome)" : all_possible_samples_text, "sample_rate" : sample_rate,"prob" : [0.1 for i in range(len(sample_rate))]})
sample_rate_dist

	sample(outcome)	sample_rate	prob
0	철수,영이,둘리	2/3	0.1
1	철수,영이,흥민	2/3	0.1
2	철수,영이,연경	1	0.1
3	철수,둘리,흥민	1/3	0.1
4	철수,둘리,연경	2/3	0.1
5	철수,흥민,연경	2/3	0.1
6	영이,둘리,흥민	1/3	0.1
7	영이,둘리,연경	2/3	0.1
8	영이,흥민,연경	2/3	0.1
9	둘리,흥민,연경	1/3	0.1

크기가 5인 모집단에서 크기가 3인표본을 추출할 때, 특정한 하나의 표본이 추출될 확률(단,단순임의추출을 했다고 가정)?
- 1. 가능한 표본이 \({10}\choose{3}\) = 10이고
- 1. 단순임의추출 : 각표본을 추출할 확률은 모두 동일하므로 \(0.1\)

\[ \begin{aligned} &P(철수,영이,둘리) = P(철수,영이,연경) = \dots = P(둘리,흥민,연경) = 1 \\ &\Leftrightarrow10P = 1 \\ &\Leftrightarrow P = 0.1 \end{aligned} \]

확률과정론으로부터 얻은 지식…
- \(P(\hat{\theta} = \frac{2}{3}) = P(\{\omega : \hat{\theta}^{-1}(\omega) = \frac{2}{3} \})= 0.6\)
  - i.e. 표본통계량 = \(\frac{2}{3}\)이 가능한 outcome(sample)은 총6가지 경우이며 확률은 각각 1이므로 \(6 \times 0.1 = 0.6\)
- \(P(\hat{\theta} = 1) = P(\{\omega : \hat\theta^{-1}(\omega) =1\}) = 0.1\)
  - i.e.(표본통계량 = \(1\)이 가능한 outcome은 1가지 경우여서 확률은 0.1
- \(P(\hat{\theta} = \frac{1}{3}) = P(\{\omega : \hat{\theta}^{-1}(\omega) = \frac{1}{3} \})= 0.3\)
  - i.e. 표본통계량 = \(\frac{1}{3}\)이 가능한 outcome(sample)은 총3가지 경우이며 확률은 각각 1이므로 \(3 \times 0.1 = 0.3\)
따라서 정확한 \(\hat\theta\)의 분포는

\(\hat\theta\)	\(\frac{1}{3}\)	\(\frac{2}{3}\)	1
\(P\)	0.3	0.6	0.1

통계량의 경험적 분포

사실 통계량의 정확한 분포를 구하는 것은 불가능하다.
- 실제 문제에서는 모집단을 정확히 모르며 하나의 표본이 주어지기 떄문이다.(대부분) \(\to\) 따라서 단순임의추출을 통해 가능한 sample(outcome)을 모두 아는 것이 불가능
- 정확히 안다고 가정해도 모집단의 크기가 너무 크면 불가능하다. \(\to\) 가능한 모든 sample(outcome)의 조합이 너무 많기에 연산복잡도가 너무 크다.
일단 이 포스팅에서는 모집단은 정확히 알고 크기가 너무 큰 경우에 통계량의 분포를 구해보는 과정을 다룬다.
모집단의 크기가 너무 크다.
\(\to\) 가능한 모든 표본의 수가 \({N}\choose{n}\) 개이다.
\(\to\) 가능한 모든 표본으로부터 통계량을 구하는 것은 컴퓨터로도 처리하기 어렵다
정확한 표본통계량의 분포를 구하기 힘드니까 근사적으로라도 구할 수 없을까?
목적
- 표본통계량의 정확한 분포는 구할 수 없으므로 표본통계량의 분포를 (근사적으로) 구한다.
- 근사적으로 구한 분포로부터 표본통계량의 확률적 성질,특징을 알아볼 수 있다.
How? : 경험적 분포를 구한다.

(경험적 분포를 구하는 과정)
- 문제 : 모집단의 크기 N = 10000이고 표본의 크기 n=100으로 할 때, 표본통계량(지지율)의 분포는 어떻게 되는가? 1. 모집단으로 부터 크기가 100인 표본을 임의추출 한다.(기억,랜덤샘플링,임의추출) 2. 표본으로부터 표본통계량 \(\hat\theta\)을 계산하고 기록한다. 3. 1,2,를 여러번 반복한다. - 일반적으로 500이상 - 예를 들어 500번 반복하면 \(\hat\theta_1,\hat\theta_2,\hat\theta_3...\hat\theta_{500}\)을 얻었을 것이다. 4. 위에서 얻은 여러 개의 표본통계량으로 부터 경험적 분포를 구한다.

위와 같은 과정을 모의실험이라고 하며 모의실험을 통하여 얻은 분포를 경험적 분포라 한다.
표본통계량의 경험적 분포는 정확한 분포와 매우 유사하다.
따라서 표본통계량의 정확한 분포를 구할 수 없는 경우 표본통계량의 경험적 분포를 통하여 확률적 성질,특징을 알아볼 수 있다.

구현

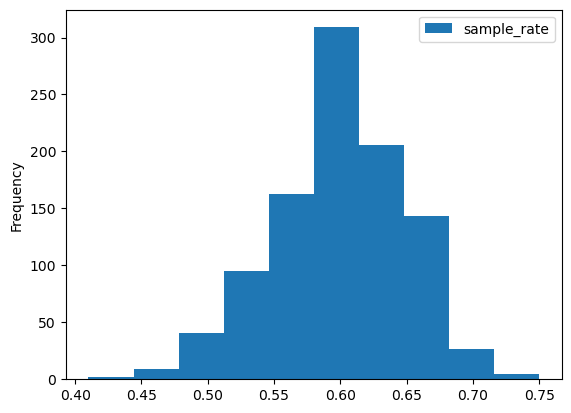
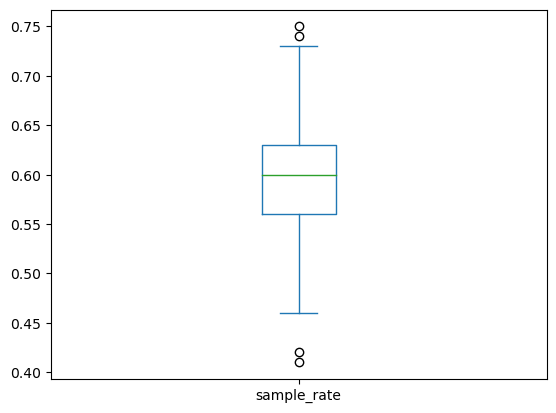
지지율이 60%인 모집단이 있다고 할 때
모의실험을 통해 크기가 100인 표본지지율의 경험적 분포를 구해보자.

# 모집단을 만든다.
P = np.concatenate((np.ones(6000), np.zeros(4000)), axis=0)
np.mean(P)

0.6

모집단 \(P\)는 np.array이다.
따라서 단순임의추출하려면 np.random.choice사용

B=1000
n=100

simulation_sample_rate = pd.DataFrame({"sample_rate":np.zeros(B)})
for i in np.arange(B):
  sample = np.random.choice(P,n,replace=False)
  simulation_sample_rate.loc[i,"sample_rate"] = np.mean(sample)
simulation_sample_rate

	sample_rate
0	0.64
1	0.60
2	0.60
3	0.60
4	0.58
...	...
995	0.62
996	0.64
997	0.68
998	0.60
999	0.55

1000 rows × 1 columns

확인

simulation_sample_rate.plot.hist()

<AxesSubplot:ylabel='Frequency'>

simulation_sample_rate.plot.box()

<AxesSubplot:>

예제 : 공공자전거 자료에서 표본평균의 분포

url1 = "https://ilovedata.github.io/teaching/bigdata2/data/seoul_bike_201909_3.csv"
bike = pd.read_csv(url1, encoding="CP949")

bike.head(10)

	자전거번호	대여일시	대여 대여소번호	대여 대여소명	대여거치대	반납일시	반납대여소번호	반납대여소명	반납거치대	이용시간	이용거리
0	SPB-17003	2019-09-28 16:10:55	368	SK 서린빌딩 앞	4	2019-09-28 17:03:32	2002	노들역 1번출구	14	52	8940.0
1	SPB-14405	2019-09-28 16:48:16	2024	상도역 1번출구	3	2019-09-28 17:03:44	2002	노들역 1번출구	18	15	1910.0
2	SPB-18431	2019-09-28 16:59:54	2002	노들역 1번출구	10	2019-09-28 17:03:57	2002	노들역 1번출구	10	2	30.0
3	SPB-04853	2019-09-28 15:31:49	207	여의나루역 1번출구 앞	32	2019-09-28 17:10:12	2002	노들역 1번출구	19	98	9610.0
4	SPB-11122	2019-09-28 15:35:41	207	여의나루역 1번출구 앞	14	2019-09-28 17:10:37	2002	노들역 1번출구	18	90	9450.0
5	SPB-23089	2019-09-28 17:02:37	2003	사육신공원앞	5	2019-09-28 17:13:44	2002	노들역 1번출구	10	10	1410.0
6	SPB-15669	2019-09-28 16:17:54	2213	고속터미널역 5번출구 앞	7	2019-09-28 17:14:22	2002	노들역 1번출구	8	56	0.0
7	SPB-09727	2019-09-28 17:04:56	2002	노들역 1번출구	5	2019-09-28 17:17:10	2002	노들역 1번출구	17	11	380.0
8	SPB-10053	2019-09-28 16:59:45	2002	노들역 1번출구	3	2019-09-28 17:17:53	2002	노들역 1번출구	5	17	1080.0
9	SPB-14487	2019-09-28 16:01:41	2024	상도역 1번출구	5	2019-09-28 17:20:44	2002	노들역 1번출구	14	78	13870.0

bike.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 407589 entries, 0 to 407588
Data columns (total 11 columns):
 #   Column    Non-Null Count   Dtype  
---  ------    --------------   -----  
 0   자전거번호     407589 non-null  object 
 1   대여일시      407589 non-null  object 
 2   대여 대여소번호  407589 non-null  int64  
 3   대여 대여소명   407589 non-null  object 
 4   대여거치대     407589 non-null  int64  
 5   반납일시      407589 non-null  object 
 6   반납대여소번호   407589 non-null  int64  
 7   반납대여소명    407589 non-null  object 
 8   반납거치대     407589 non-null  int64  
 9   이용시간      407589 non-null  int64  
 10  이용거리      407589 non-null  float64
dtypes: float64(1), int64(5), object(5)
memory usage: 34.2+ MB

bike.describe()

	대여 대여소번호	대여거치대	반납대여소번호	반납거치대	이용시간	이용거리
count	407589.000000	407589.000000	407589.000000	407589.000000	407589.000000	407589.000000
mean	1880.239587	7.180022	2513.636349	6.902335	30.156827	4253.336228
std	878.719112	5.262180	714.170698	4.898559	32.065934	5782.673901
min	101.000000	1.000000	2002.000000	1.000000	1.000000	0.000000
25%	1233.000000	3.000000	2177.000000	3.000000	8.000000	1200.000000
50%	2171.000000	6.000000	2303.000000	6.000000	18.000000	2380.000000
75%	2313.000000	10.000000	2619.000000	10.000000	43.000000	5130.000000
max	99999.000000	40.000000	99999.000000	39.000000	2479.000000	153490.000000

bike.shape

(407589, 11)

2019년 9월 동안 서울특별시 공공자전거 대여 이력 자료
2019년 9월 동안 서울특별시 공공자전거 대여 이력을 모두 모아놨으므로 모집단이다.
관심있는 모수 : 이용거리의 평균
공공자전거 모집단에서 표본을 simple random sampling without replacement으로 여러번 추출하는 경우에 표본통계량의 경험적 분포를 구해보자.
각각의 모든 표본의 크기가 최대 n=2000 개라면 표본의 크기에 비해 모집단의 크기가 상대적으로 매우 큼을 알 수 있다.
이때 다음과 같은 주목할 만한 사실이 있다.
- 이 경우 비복원추출과 복원추출의 차이가 거의 없다.
  - 복원추출과 비복원추출의 차이점은 한 번 뽑힌 개체가 또다시 뽑힐 수 있느냐는 것이다.
  - 그러나 이 경우는 비복원추출을 해도 모집단이 너무 크기에 사실상 한 번 뽑힌 개체가 다시 뽑힐가능성이 매우작다.(0은 아니다.)
  - 따라서 다시 뽑힐 가능성을 0으로 두고 하는 복원추출과 이 경우의 비복원추출은 사실상 같다.

B = 1000, n = 50인 경우 표본비율의 경험적 분포.

B=1000
n=50

sample_means_50 = pd.DataFrame({"sample_means":np.zeros(B)})
for i in np.arange(B):
    sample_means_50.loc[i,"sample_means"] = bike.sample(n=n,replace=False)["이용거리"].mean() 
    #이 부분 sample하고 column index위치 바꾸면 안됨
sample_means_50

	sample_means
0	6331.6
1	3449.2
2	3372.0
3	4369.2
4	3487.6
...	...
995	4048.8
996	5155.4
997	4827.6
998	4630.6
999	3173.8

1000 rows × 1 columns

sample_means_50.plot.hist(y="sample_means")

<AxesSubplot:ylabel='Frequency'>

sample_means_50.plot.box(y="sample_means")

<AxesSubplot:>

B=1000,n=1000 표본비율의 경험적 분포

B=1000
n=1000

sample_means_1000 = pd.DataFrame({"sample_means" : np.zeros(B)})
for i in np.arange(B):
    sample_means_1000.loc[i,"sample_means"] = bike.sample(n=n,replace=False)["이용거리"].mean()
sample_means_1000

	sample_means
0	4415.75
1	4384.23
2	4409.41
3	3903.12
4	4010.64
...	...
995	4464.98
996	4361.14
997	4693.28
998	4451.37
999	4372.24

1000 rows × 1 columns

sample_means_1000.plot.hist(y="sample_means")

<AxesSubplot:ylabel='Frequency'>

sample_means_1000.plot.box(y="sample_means")

<AxesSubplot:>

\(n= 50\) vs \(n = 1000\)

f,ax = plt.subplots(1,2,figsize=(20,10))

plt.subplot(1,2,1)
plt.boxplot(sample_means_50)
plt.hlines(y=4253.336228, xmin=0.5, xmax=1.5, colors='r')
plt.ylim(2000,9000)

plt.subplot(1,2,2)
plt.boxplot(sample_means_1000)
plt.hlines(y=4253.336228, xmin=0.5, xmax=1.5, colors='r')
plt.ylim(2000,9000)

(2000.0, 9000.0)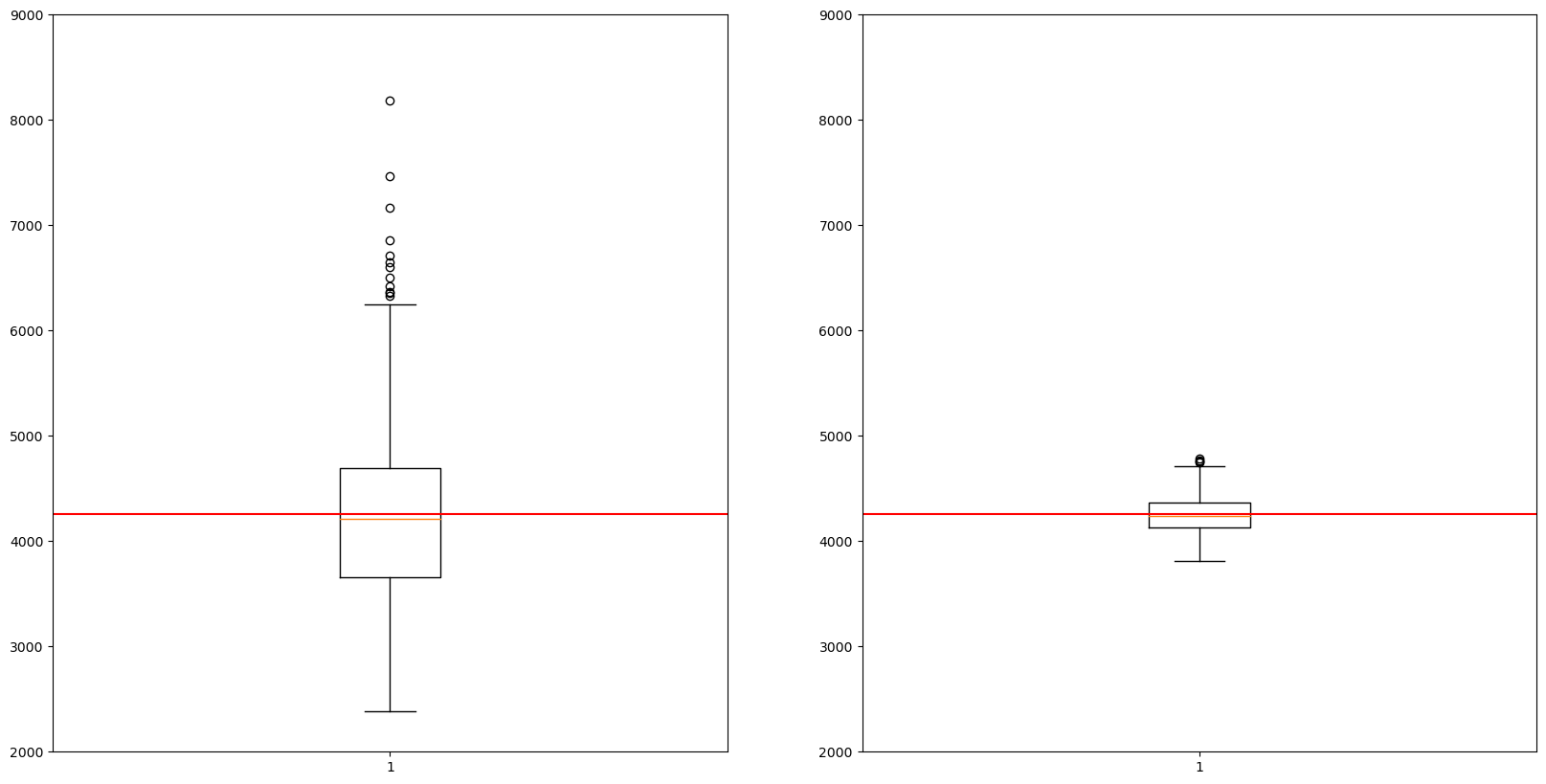

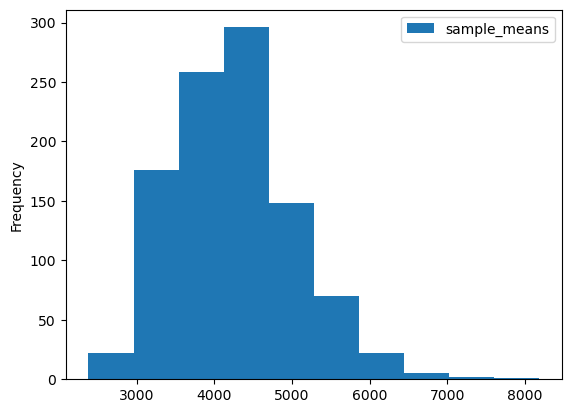
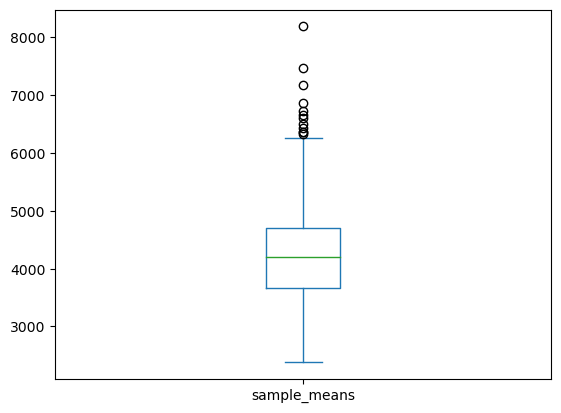
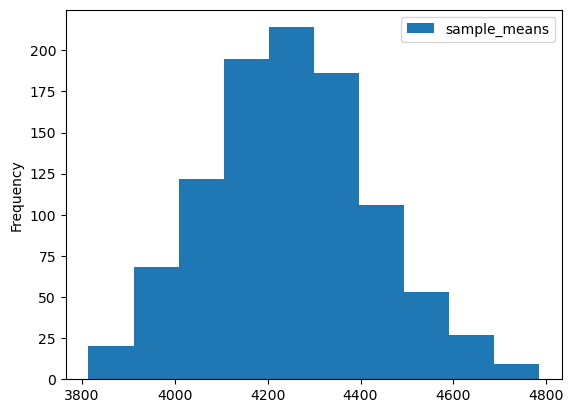
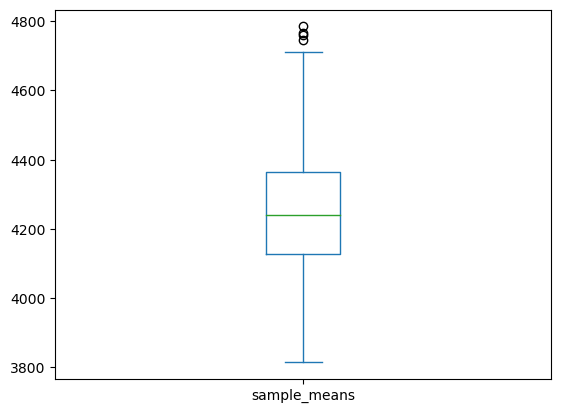
plt.hist(sample_means_50,bins=50)
plt.hist(sample_means_1000,bins=50)
plt.show()

표본의 크기가 1000인 경우 표본평균의 경험적 분포는 50인 경우보다 좌우 대칭인 종모양(정규분포)에 더 가까워 보인다.
표본의 크기가 1000인 경우 표본평균의 경험적 분포는 50인 경우보다 분산이 작음.

뭔가 규칙이 있는 거 같다. 표본의 크기 n이 커질수록 표본평균의 분포가 정규분포에 가깝고 분산이 적은거 같은데?
프로그래밍으로 확인해보자~

B = 1000
sample_sizes = [10,20,100,400,900,1200,1500,1800,2000]
total_num = B * len(sample_sizes)

emprical_dists=pd.DataFrame({"sample_size" : np.zeros(total_num),"sample_means" : np.zeros(total_num)})
count = 0
for n in sample_sizes:
    for i in np.arange(B):
        emprical_dists.loc[count,"sample_means"] =  bike.sample(n=n,replace=False)["이용거리"].mean() #means아니라 mean
        emprical_dists.loc[count,"sample_size"] =  n #means아니라 mean
        count+=1
emprical_dists.head(10)

	sample_size	sample_means
0	10.0	3517.0
1	10.0	3405.0
2	10.0	4661.0
3	10.0	3394.0
4	10.0	3390.0
5	10.0	3850.0
6	10.0	4766.0
7	10.0	3616.0
8	10.0	3018.0
9	10.0	2743.0

sns.boxplot(x=emprical_dists["sample_size"],y=emprical_dists["sample_means"])
plt.ylim(1000,12000)

(1000.0, 12000.0)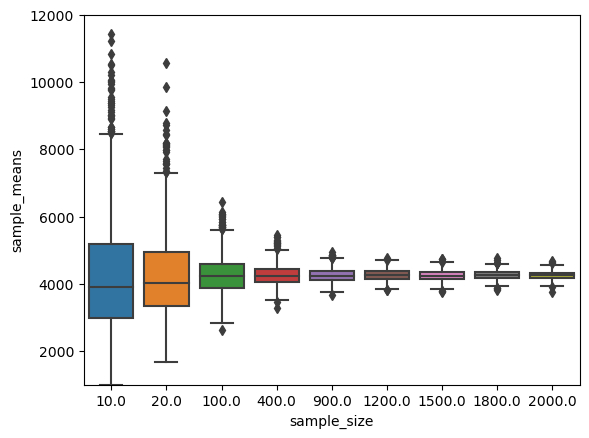

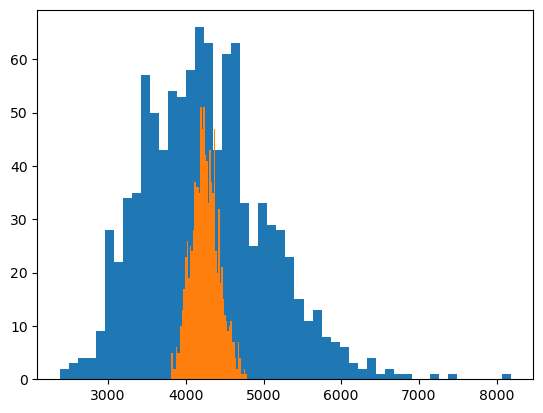
plt.hist(emprical_dists.loc[emprical_dists.sample_size==900,"sample_means"],color="blue",bins=15)
plt.hist(emprical_dists.loc[emprical_dists.sample_size==1500,"sample_means"],color="green",bins=15)
plt.hist(emprical_dists.loc[emprical_dists.sample_size==2000,"sample_means"],color="red",bins=15)
plt.show()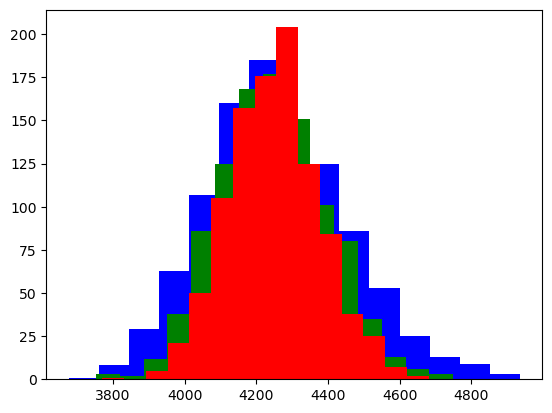

box,hist plot으로부터
- 1. 표본의 크기 n이 클수록 표본평균의 분포가 정규분포로 가까워 지는 것처럼 보이고
- 1. 그때의 분산도 작아지는 것을 확인할 수 있다.
사실 이 정리는 중심극한정리이다..!

정리

표본통계량의 분포를 구하는 것은 중요하다.
- 모수를 구하는데에 핵심적인 정보이기에 특징,성질을 파악해야하고
- 추후에 나올 방법에 사용되기 때문이다.
하지만 정확하게 구하는데에는 한계가 있다.
1. 실제 문제에서는 모집단을 정확히 모르며 하나의 표본이 주어지기 떄문이다.(대부분) \(\to\) 따라서 단순임의추출을 통해 가능한 sample(outcome)을 모두 아는 것이 불가능
2. 정확히 안다고 가정해도 모집단의 크기가 너무 크면 불가능하다. \(\to\) 가능한 모든 sample(outcome)의 조합이 너무 많기에 연산복잡도가 너무 크다.
따라서 이번 포스팅에서는 모집단을 정확히 아는 경우에 한해서 정확한 분포를 근사하는 경험적분포를 통해 표본통계량의 분포를 구했다.
분포를 구해본 결과 그 과정에서 표본의 크기가 커질수록
- 정규분포에 가까워지고
- 분산이 작아졌다.
- 이는 사실 중심극한정리(CLT)이다.
여기까지 이번 포스팅의 내용..
하지만 실제문제상황에서 우리에게 주어지는 것은 단 하나의 표본뿐이다.
이러한 상황에서는 표본통계량의 분포를 어떻게 구하는가? … 다음 포스팅에서 …